Abstract

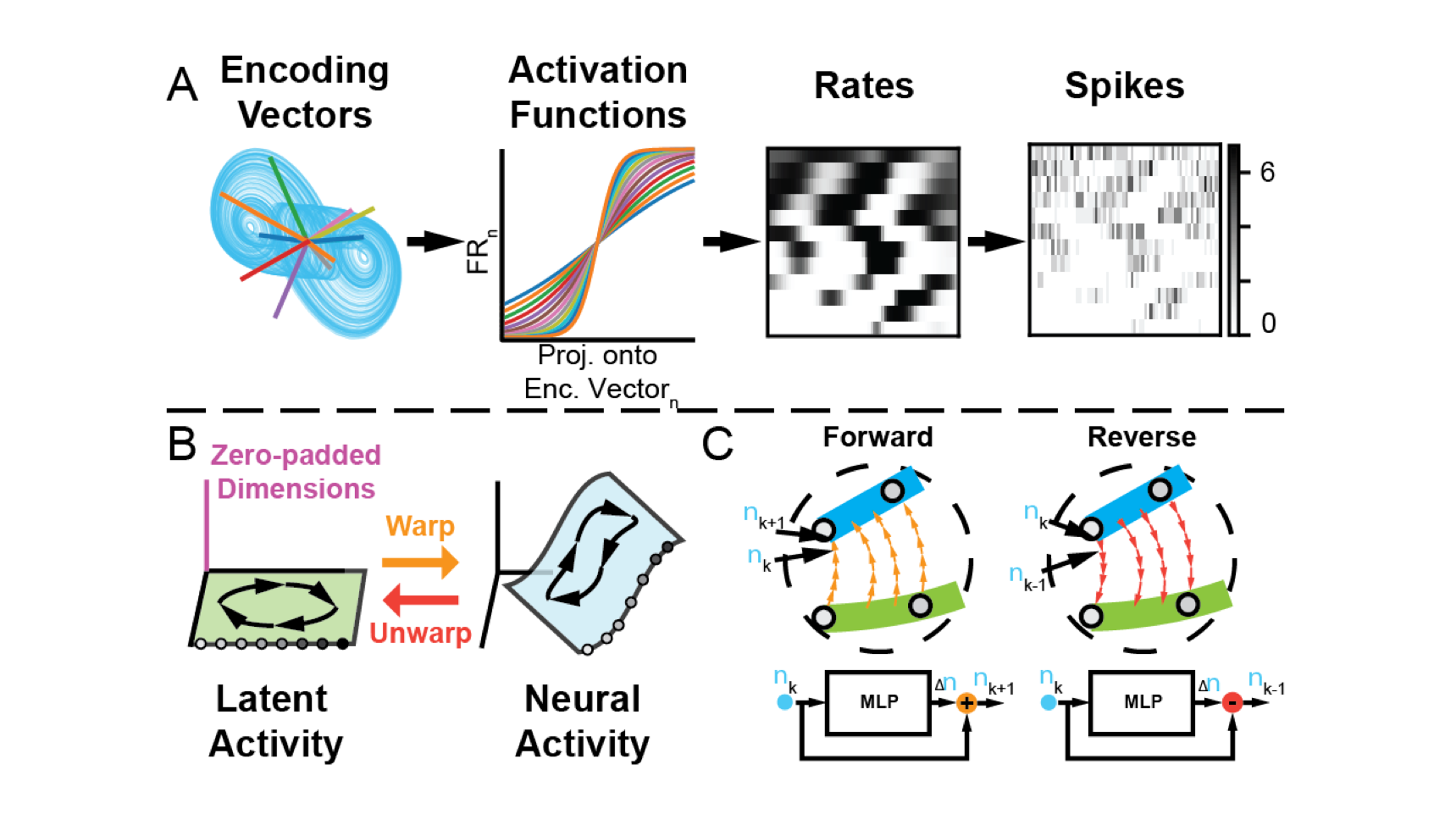
The advent of large-scale neural recordings has enabled new methods to discover the computational mechanisms of neural circuits by understanding the rules that govern how their state evolves over time. While these \textit{neural dynamics} cannot be directly measured, they can typically be approximated by low-dimensional models in a latent space. How these models represent the mapping from latent space to neural space can affect the interpretability of the latent representation. We show that typical choices for this mapping (e.g., linear or MLP) often lack the property of injectivity, meaning that changes in latent state are not obligated to affect activity in the neural space. During training, non-injective readouts incentivize the invention of dynamics that misrepresent the underlying system and the computation it performs. Combining our injective Flow readout with prior work on interpretable latent dynamics models, we created the Ordinary Differential equations autoencoder with Injective Nonlinear readout (ODIN), which captures latent dynamical systems that are nonlinearly embedded into observed neural activity via an approximately injective nonlinear mapping. We show that ODIN can recover nonlinearly embedded systems from simulated neural activity, even when the nature of the system and embedding are unknown. Additionally, ODIN enables the unsupervised recovery of underlying dynamical features (e.g., fixed points) and embedding geometry. When applied to biological neural recordings, ODIN can reconstruct neural activity with comparable accuracy to previous state-of-the-art methods while using substantially fewer latent dimensions. Overall, ODIN's accuracy in recovering ground-truth latent features and ability to accurately reconstruct neural activity with low dimensionality make it a promising method for distilling interpretable dynamics that can help explain neural computation.